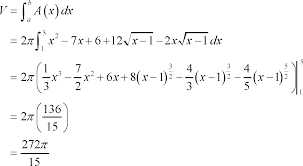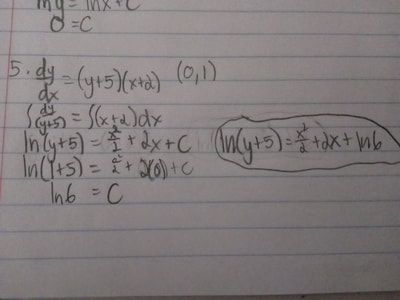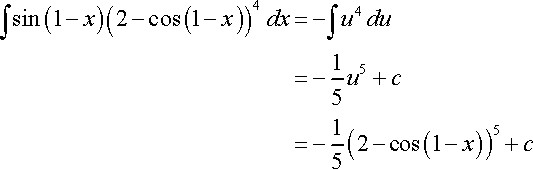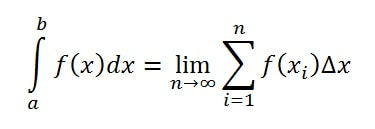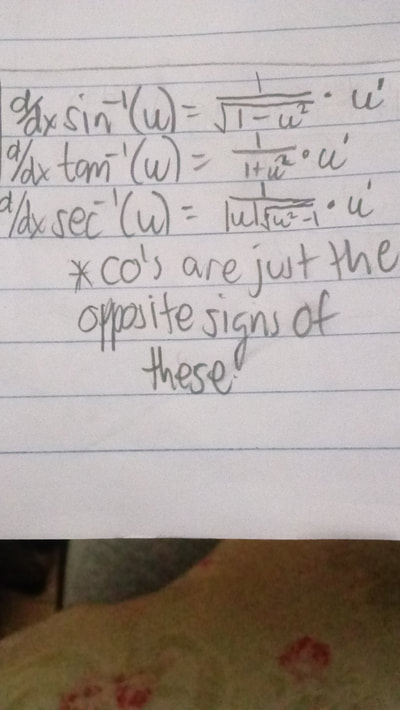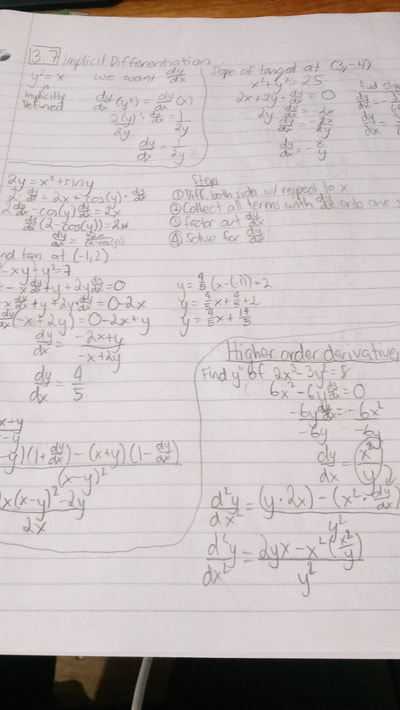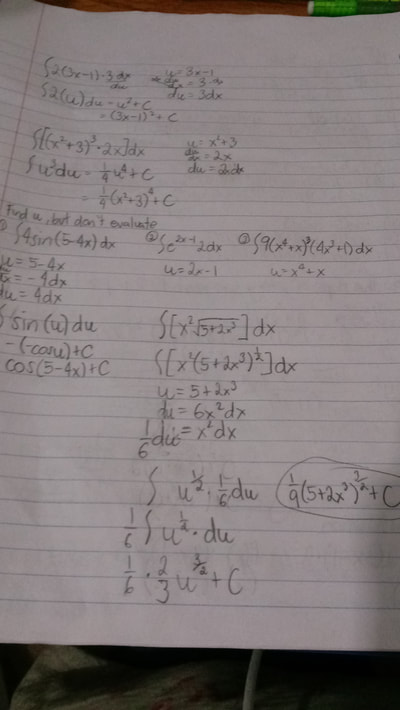|
Time to learn about some applications of integrals in the context of the volumes of curves.
This week we talked about how to find the volume that a curve has with respect to either the Y-axis or the X-axis, which depends on how the equations are set up or how the curves themselves are oriented. We also took a quiz on how to use the integral in order to find the area in between two curves on Wednesday. I thought the quiz wasn't THAT hard. But I did realize that I messed up on two of the problems right after I turned it in. Like literally, right as I set the freaking paper down on my teacher's desk I realized that I f-d up on a problem. Which is always a great sign right? Talking about the volume under a curve stuff. We can use the integral of a function in order to find the volume of the curve when it is spun around either the x or y axes. What you have to do is just basically use the integral notation, put in the bounds of the function, plug in the area function of the solid that is formed once the curve is spun around the axes, then just used NINT on your calculator. Or you can do it manually, but who wants to do that?
0 Comments
Oh boy, this week I learned about how to use definite integrals to find the are in between curves.
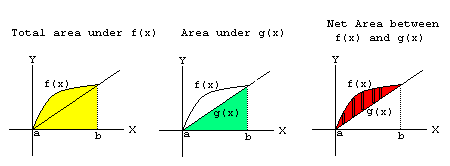
It was a fairly easy concept to grasp and I feel like I understand it well enough to the point of not needing to consult my pink sheet for help during the quizzes that we're eventually going to take. But I probably still consult it since I don't really trust what I can remember off the top of my head all that much. In terms of what the applications of definite integrals entail, well it's basically just using the integrals in story problems nothing more nothing less. The concept that I actually liked to do this week was finding the area in between two curves. This is because it is not only easy to do, but it also makes sense to me as to why we do it the way we do. To find the area in between two curves the first thing you need to do to figure out which curve is always on op or the other, then get the equation of that curve and subtract the integral of the equation of the other curve from its integral. Then BAM you've got your area. This week we start off learning about the wonderful idea of "Slope Fields" and halfway through the said week, we have a quiz on 6.1 and 6.2. After that was all over with we start learning about the new concept called: "Separable Differentiable Equations."
To be honest, when I first so what Slope Fields actually meant I was very turned off by it because of how simple it seemed to look and how it was just basically drawing in estimates of what you think the slope would look in that exact point in the graph. But it was more than that, Slope Field problems gives you a derivative equation and you have to figure out the slopes of each point by plugging in x and y value at an exact point. It is rather tedious because you have to do this for EVERY POINT IN THE GRAPH. Well I guess it isn't all bad since there was often a pattern to how the slopes were going to go. But when there wasn't, it was a pain. But yeah, Slope Fields are pretty easy. Like I said in the beginning we took a quiz on the 6.1 and 6.2 sections that we learned. I didn't think it was that hard. But then again, after I get the quiz I'll probably some stupid mistakes that I made that caused me to lose points. It's pretty sad how I already expect it to happen, but I know it will so might as well be ready for it. Before we ended the week, we learned about the idea of "Separable Differentiable Equations." It basically looks the same as Implicit Differentiation, except you're gonna have to anti-derive at some point and arrive at an answer that looks like a potential original function for the derivative given. Okay so this week we get visited by our old friend "U" Substitution. That wonderful being that helped with anti-deriving all those weeks before...... I still hate it.
So we basically had to re-learn how to do "U" Substitution because it has been quite a while since the last time we all had to do it. While doing the problems for review, I was reminded of how much I loathed doing "U" Substitution. Not just because of how tedious it gets, because a lot of math aspects get tedious, but it was also because of how I was still confused on the whole 'choosing which to use for the "u"' thing. I understand it a lot better now, and a lot of it is just guess and check for me right now until I get used to doing it a lot more through the homework assignments that we got during the week. We're gonna have a quiz over everything that we learned next Wednesday so that's gonna be fun to see if I actually understand how to do and use "U" Substitution properly now. This week in AP Calculus, we learned how to find the area under a curve. Approximate and exact, well as exact as we can possibly get. USING RECTANGLES!!
First we learned about RRAM, MMRAM, and LRAM. No, not the computer kind of RAM. I'm talking about the Rectangular Approximation Method. There's three types because there's three ways that you could use this RAM. You can use it by having the right side, left side, or middle of the rectangle hitting the curve. Whichever one you use, the most accurate would be the MRAM, or by drawing the middle of the rectangle witting the curve. This is because of the amount of wasted space that does not get accounted for in the calculation of the area when using LRAM and RRAM. Aside from the RAM stuff, we learned more uses for the sigma notation and the integral stuff. We learned that you can find the area under a curve by using Integrals.. WOW. Overall I didn't think that the concepts were hard. They were pretty easy to grasp and understand. They're nothing like optimization and related rates that's for sure. It's been a good long while since the last time I have put out a blog post for AP Calc.
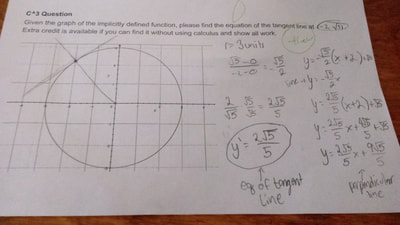
This week started off pretty interestingly. This is because of the quiz that we had last Friday about the subject of Optimization. Before taking the quiz I was positive that I knew how to do optimization problems and that I understood it very well. Well, it turns out that I actually did not understand the subject fully. When we got the quiz on Friday, I stared at it for a good long while before I actually started doing it. I looked at the four problems and was essentially lost on how to start them. After like 5 mins, I decided to actually start the thing and when I read the first problem, it wasn't that bad. It was like one of the simpler problems that involved Optimization. The second one got me really confused, and after getting the quiz back i found that I just read the problem wrong, so that sucks. For the third question i forgot to plug the value for X that I had found back into the model equation to find the time value. And, I just left the 4th question blank because I actually had no idea on how to even start the problem. Before we got the quizzes back, we all got a message from our teacher stating that he apologizes if we see any tear stains on our quizzes. I felt really bad because I felt like he explained the concept really well, and that I just didn't put in the effort to further that general understanding. Getting away from that awful quiz experience, we started a new lesson for this week. This was Related Rates. After our teacher finished explaining what the concept was, I felt like this was a lot more simpler to understand and do than Optimization for me. it made a lot more sense and I could understand what i was doing the whole time. I was legit happy because this meant that I could do the homework problems with no problem at all, and that was the case. Though the questions did get a bit more difficult over time, it didn't get as difficult as most of the Optimization problems did. Overall I think that the main difficulty that comes with learning Optimization and Related Rates is the setup and finding the right equations to use for each problem. This fact is especially hard for me because there are so many possibilities that I just get even more confused on which one to actually use. But, i found that I should just take the time to try each and every possibility, this not only gives me practice but also insight on how to do the problem itself. This week we started off with the Chain Rule, "U" Substitution, and Implicit Differentiation quiz. Overall, I didn't think that the quiz was necessarily any harder than the problems that we've had to do in the homework that we get. Once of the questions did throw me off for about 10 mins though. It had something to do with finding the equation of the tangent line at a specific point in a circle graph. I completely forgot what the equation for a circle was so I kinda got stuck for a while before I got an idea on how to do it. First I took the point that was given to me: (-2, square root(5)) and used the origin (0, 0) as the second point. Then, I found the slope of the line that connected those two points. Then I took the perpendicular slope of that line and found the equation for it. Lastly, I just found the derivative of the perpendicular line to find the slope of the tangent line. When i got the quiz back, I was so happy that I got the extra credit involving not using calculus in it.
To what we actually learned this week, NEW DERIVATIVES!! How exciting. So we basically just learned the derivative of the inverse trig functions (sin^-1(x), cos^-1(x)...etc). They basically share the same process in differentiation as the other derivatives so it wasn't that hard to grasp. Though, i did find that having the square roots a part of the actual derivative function to be a confusing part of the whole thing. I just hate dealing with square roots, i get confused whenever i try to string it out farther. The last thing that we learned was how to derive exponential functions (e, ln, and log). Just like the trig functions, they're basically the same process. Overall I thought that the stuff that we learned this week weren't really that challenging. But I guess we'll just have to see how I actually do during the Chapter 3 test that we'll be having next Wednesday. This week we started talking about the anti-derivative version of the Chain Rule.... "U" Substitution. We also talked about the topic of Implicit Differentiation towards the end of the week. They were both just expanding upon the idea of derivatives and differentiation so I guess it shouldn't be that hard if you fully understood the past concepts. So basically spent the whole week learning and reviewing for the upcoming quiz on Monday about this stuff.
"U" Substitution is when you identify which is the inside part of a chain rule derived function and substitute the letter "u" for that whole part. Then, find the derivative of that inside function and label it as "du" and substitute that in also. It gets kind of convoluted when you start getting a constant or a term that does not match what the original derived function has so then you would have to divide to have "du" or "dx" alone then substitute them back in. After learning this rule for the first time, I was lost as heck. I understood it to the substitute for "u" part, but then when it came to the "du" stuff, I got lost. But, i think doing the homework and more practice has helped me understand it better. Expecially the mini quiz that we did half way through the week to check our understandings on Chain Rule, "U" substitution, and anti-deriving in general. The next topic that we learned and talked about what Implicit Differentiation. This is basically saying that you have to derive both sides of an implicitly defined equation. For example, in y^2=x you would start with having 2y*dy/dx=1. This is because you derive both the left and the right side. But the catch is that whenever you derive something with a variable y in it, don't forget to use dy/dx for it. The main objective of this is to collect all terms with dy/dx's on them to one side then go from there. It doesn't get any different when we start talking about high order derivatives for implicitly defined functions, because the only difference is that you would have to do it twice and substitute the value for dy/dx back for the answer if you need it. This was way easier to understand than the "u" substitution, but I guess it's because it's more of just basically a collection of everything that we've been doing so far and less of new concepts. I feel like I'm going to be more or less ready for the upcoming quiz on Monday, I just need to practice more during the weekend. This week we learned something new, called the CHAIN RULE!!
Before I go into the Chain Rule, I'm going to talk more about what else we did this week. We started off the week with basically a review day since there was going to be our inevitable section 3.3 and 3.5 quiz the following day. Just to re-cap section 3.3 dealt with how to find the derivatives of functions by hand using the rules that were presented to us by Mr. Cresswell. Overall, I thought that the rules were very easy to grasp and that I understand them very well. Doing the rules only gets dumb when the functions start to become more complex. For example, a function might have a product rule and a quotient rule worked in it before you could even get to the derivative. At that point it just gets to be a pain, but what makes it worse it that you can't even bank on the fact that it might simplify beautifully at the end so it just looks like you have the wrong answer just because it looks ugly to look at. Oh yeah, anti-derivatives were a thing in section 3.3 also. It's basically going backwards from a derivative to it's original function. I didn't find this concept to be particularly hard. Section 3.5 then adds the trig functions into the derivative mix. Not any different really, except for the fact that you're dealing with sine, cosine, and tangent. Now section 3.6 was a doozy. It was the Chain Rule. Which apparently was important enough for it to deserve it's own section, unlike the other rules. But, after working with the Chain Rule for about 4 days I can say that it deserves that honor very much. At first glance, you could say that the concept isn't really that hard to grasp, which it isn't. But then it gets really convoluted when you add the other rules into play, in one function. So you could have a function that you need to do a quotient rule to find the derivative, but within that there is a product rule that you have to do, THEN you have to do the Chain Rule to finish everything off. So that's basically how hard it gets, which sometimes just fills up an entire page. I do understand the basic concept of the Chain Rule and I just need more practice to get used to the longer chains. So since Mr. Cresswell decided to give us a break the week before and decided not to have our 3.1-3.2 quiz last Friday, we had to then take it on Monday. We kicked the calculus week off with a quiz... off to a great start. Considering how we had Homecoming weekend just happened, it's suffice to say that a lot of people didn't really prepare for this quiz that much. So i don't know how I feel about that weekend break and not doing the quiz on that Friday, but i guess the time restraints on that Friday was an issue due to the homecoming assembly so i understand where Mr. Cresswell was coming from when he made that decision.
Through the rest of the week though, we started sections 3.3 and 3.5 which dealt with anti-derivatives and derivatives of trigonometric functions. For the anti-derivatives, I didn't really find them to by that difficult, quite straightforward actually. With all the different rules present I just have to remember what they mean and what it means to do them at the same time. The way Mr. Cresswell explained the rules really helped me understand them well, it was just annoying that a lot of people in the class were being chatty and annoying, but whatever, I got what I wanted out of the lesson and that was to understand the rules for anti-derivatives so I'm happy. As for the derivatives of trigonometric functions, they were all basic derivative stuff but with trig. so it wasn't really a tough topic to absorb. To finish off the week I just need to finish all the different book homework and worksheets that we were handed out to us. All I really need to finish is the anti-derivative worksheet and I'm good for the week, so I'm happy. Overall I felt that the week went by really smoothly, except with seeing my grade on the quiz that we took on Monday. but I plan on retaking that since I know that I can do better and I am very disappointed in myself about that grade. |
AuthorBryll Matthew Moreno |